I modelli qui presentati offrono un metodo semplice, ma accurato per stimare la resistenza aerodinamica che agisce sugli sciatori, mentre si spostano lungo il pendio attraverso la gamma di posizioni tipiche dello sci. Gli atleti che praticano discipline come la corsa, il pattinaggio di velocità, il ciclismo o lo sci di fondo sono sempre stati interessati ad ottimizzare la loro resistenza aerodinamica per aumentare la velocità e ottenere prestazioni migliori (8, 14, 15, 18). Nello sci alpino la forza gravitazionale viene utilizzata per aumentare l’energia cinetica dello sciatore, mentre la resistenza aerodinamica è una delle due forze, non conservative, che svolgono un lavoro negativo sullo sciatore. La quantificazione di questo parametro è quindi importante per comprendere le prestazioni degli sciatori.
Diversi studi hanno esaminato la resistenza aerodinamica dello sciatore:
- Watanabe e Ohtsuki (19, 20) hanno analizzato la resistenza aerodinamica di una varietà di posture sciistiche in uno studio in galleria del vento e la velocità sugli sci, in uno studio sul campo;
- Kaps e altri (7) hanno proposto un metodo per calcolare l’attrito della neve e la zona di resistenza (CDA) durante lo sci alpino, usando fotocellule;
- Savolainen (12) ha condotto un’analisi teorica della resistenza per confrontare la postura di diversi sciatori e determinare i fattori che limitano la velocità;
- Luethi e Denoth (9) hanno sviluppato, con test in galleria del vento, i coefficienti di prestazione che tengono conto di fattori come la massa (M), l’area frontale (AF) e il coefficiente di resistenza (CD);
- Thompson e Friess (17) hanno eseguito test in galleria del vento per migliorare l’efficienza aerodinamica degli sciatori di velocità, ottimizzando la postura e le attrezzature.
Sebbene questi studi abbiano dato un prezioso contributo alla nostra comprensione delle proprietà aerodinamiche delle posture statiche per lo sci, sono limitati dal fatto che lo sci alpino è principalmente uno sport dinamico in cui lo sciatore si muove continuamente e cambia posizione. Per consentire l’analisi della resistenza degli sciatori che effettuano curve, Barelle e altri (2) hanno modellato il CD sulla base delle lunghezze del segmento dell’atleta e degli angoli tra i segmenti corporei, consentendo in tal modo la determinazione delle proprietà aerodinamiche, attraverso una gamma completa di posizioni tipicamente riscontrate nello sci. Tuttavia le lunghezze del segmento e gli angoli inter-segmentali richiesti per utilizzare questo modello sono spesso difficili da ottenere in contesti di ricerca sul campo.
Nonostante questi studi precedenti abbiano esaminato le proprietà aerodinamiche degli sciatori, l’importanza della resistenza aerea verso le prestazioni in questo sport dinamico è scarsamente compresa. L’energia meccanica (cioè la somma di energia cinetica e potenziale) è stata usata da Supej (16) per dedurre energia dissipata durante le curve. Reid e altri (11) hanno usato lo stesso metodo nello slalom, ma i fattori intrinseci che influenzano questa dissipazione di energia non sono stati ancora analizzati.
Il primo obiettivo di questo studio di Meyer F. e altri del 2012, è stato quello di sviluppare modelli del Coefficiente di Resistenza Aerodinamico (CD) di sciatori che eseguono delle curve.
Il secondo obiettivo di questo studio era di utilizzare i modelli sviluppati per analizzare l’energia dissipata dalla resistenza aerodinamica di uno sciatore usando una tecnica dinamica, in cui lo sciatore espone al vento un Area Frontale (AF) relativamente grande o una tecnica corporea compatta, dove lo sciatore mantiene una posizione aerodinamica, mentre esegue curve di slalom gigante su una pista da sci.
Metodi
– Esperimento in galleria del vento
Quindici sciatori di sesso maschile e femminile (media ± DS: corpo (M)= 75,9 ± 9,7 kg, altezza (H)= 1,79 ± 0,07 m, età= 32,3 ± 6,7 anni) si sono offerti volontariamente per lo studio. Tutti i partecipanti erano sani, senza problemi di movimento articolare.
I test sono stati effettuati presso l’Università di Auckland in una galleria del vento con una configurazione a getto aperto, il getto con dimensioni di 2,5 m (larghezza – W) di 3,5 m (altezza – H) e una velocità di flusso massima di 18 m/s. I livelli di turbolenza erano approssimativamente dello 0,5% nella direzione del flusso e il profilo di velocità era uniforme.
I partecipanti sono stati posizionati su una piattaforma di forza in grado di misurare la resistenza nella direzione del vento longitudinale. La forza di resistenza (D) è stata calcolata misurando lo spostamento di un blocco di forza distorta, utilizzando un trasduttore di spostamento lineare variabile (RDP, Ltd., Heath Town, Regno Unito).
Un convertitore analogico/digitale a 16 bit (NI-6034; National Instruments, Austin, TX) è stato utilizzato per acquisire il segnale su un PC a una frequenza di 200 Hz. Il trasduttore di spostamento lineare variabile è stato precedentemente calibrato su una gamma adeguata di carichi. Questo trasduttore presenta un alto grado di linearità e ripetibilità, con una precisione di circa l’1% della lettura misurata e una ripetibilità dello 0,5% (5). In conformità con Sayers and Ball (13), non sono state necessarie correzioni di flusso nelle gallerie a circuito aperto perché il modello di blocco, ovvero, la persona, era inferiore a 1 m2 e l’area aperta era di 12,25 m2.
La pressione del vento dinamica è stata registrata con un trasduttore di pressione Setra tramite una sonda statica di Pitot (Airflow Developments, Ltd., High Wycombe, Regno Unito) posizionata nella galleria del vento, a monte della sezione contratta. Prima dell’esperimento, una seconda sonda è stata posizionata nel mezzo della sezione del test per determinare il rapporto di pressione dinamica tra le due posizioni. La pressione misurata in fase di esecuzione è stata quindi regolata di conseguenza. L’accuratezza della pressione dinamica è di circa il 2% del valore misurato con una ripetibilità di circa lo 0,2%. Sono state registrate la pressione dinamica, la temperatura dell’aria e la pressione atmosferica per consentire alla resistenza di essere correttamente dimensionata.
Una limitazione con molti sistemi di gallerie del vento, è rappresentata dall’incapacità di misurare l’AF di un oggetto in movimento irregolare. Ciò consente solo di calcolare il CD, che è di utilità limitata in molti calcoli successivi. Per consentire il calcolo di un vero CD, è stato sviluppato un sistema di misurazione AF in tempo reale. Consisteva in una telecamera in miniatura (USB UI-1485LE; IDS Imaging, Obersulm, Germania) posizionata nella galleria del vento davanti del partecipante. Lo sfondo era di colore bianco e l’area coperta da ciascun pixel veniva calcolata misurando la dimensione di un oggetto di riferimento posizionato sul piano medio del partecipante.
Durante il test, il partecipante era vestito con un abito nero, che serviva sia a contrastare la fotografia, che a uniformare l’abbigliamento per le misure di resistenza. È stata effettuata una soglia del 50% sull’immagine in scala di grigi del partecipante, generando un’immagine in bianco e nero. Il numero totale di pixel neri sullo sfondo bianco è stato quindi contato e convertito in un’area reale in metri quadrati, che veniva visualizzata sul soggetto ogni 0,5 s. La precisione di questo sistema era di circa 0,001 m2. Le immagini in bianco e nero sono state anche utilizzate per determinare la H e la W degli sciatori contando il numero di pixel neri attraverso la massima distanza orizzontale e verticale tra due punti di riferimento anatomici sul piano frontale.
- Procedura sperimentale
Sono stati misurati in metri e in chilogrammi, prima del test, sia H, che M, di ciascun partecipante e la corrispondente superficie corporea (BodyS), che rappresenta l’area totale della pelle, è stata calcolata usando il metodo di Boyd (4). Per tenere conto di eventuali letture indotte dal peso, il trasduttore di forza è stato azzerato con il partecipante sulla bilancia in condizioni senza vento all’inizio di ogni prova. La massima AF (MaxA) di ciascun partecipante (in piedi con le braccia aperte) è stata misurata contemporaneamente attraverso la telecamera in miniatura. La galleria del vento è stata quindi gestita fino a una velocità di circa 16 m/s, corrispondente alla velocità solita di entrata sulla porta in condizioni di slalom gigante, e, quindi, il numero di Reynolds era approssimativamente uguale a quello che avrebbero sperimentato i partecipanti sul campo.
Dopo un periodo di prova, i partecipanti hanno assunto nove posture, con diverse flessioni dell’arto inferiore e posizionamenti dell’arto superiore (Fig. 1). Un interruttore di luce rossa/verde è stato installato davanti ai partecipanti per far loro sapere quando avrebbero dovuto cambiare postura. Ogni posizione è stata ripetuta tre volte e mantenuta per 15 secondi durante i quali sono state misurate e mediate D e AF
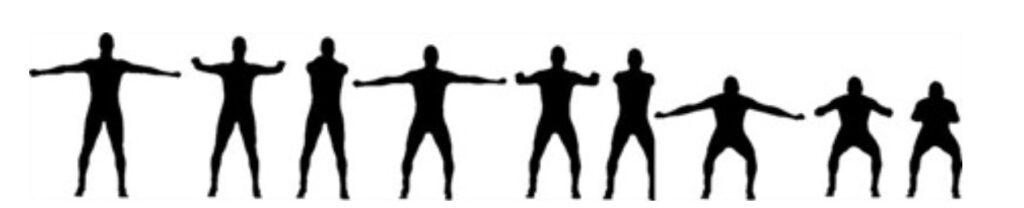
Figura 1: le nove posizioni di sciatore testate, viste dalla telecamera frontale
Il CD é stato calcolato nel modo standard come segue:
dove ρ è la densità dell’aria e V è la velocità del vento. La pressione dinamica (ρV2/2) è stata misurata con il trasduttore di pressione Setra, l’AF è stata misurata con la telecamera in miniatura e D è stata misurata con il bilanciamento della forza.
- Costruzione del modello
Quando si effettuano prove sul campo, i dati antropometrici di un partecipante potrebbero non essere sempre disponibili (come nelle impostazioni della competizione), mentre altre informazioni potrebbero essere difficili da ottenere (come la AF, che può essere ottenuta solo da immagini frontali complete). Pertanto sono stati costruiti modelli basati su diverse combinazioni di parametri (da due a sette), per accogliere le informazioni normalmente disponibili nelle condizioni di prova sul campo.
Sulla base delle possibili serie di dati disponibili, sono stati creati sei modelli: quattro modelli generalizzati che utilizzano tutti i dati dei partecipanti, nonché due modelli individualizzati per ciascun partecipante. La tabella 1 riassume i parametri utilizzati in ciascuno dei sei modelli.
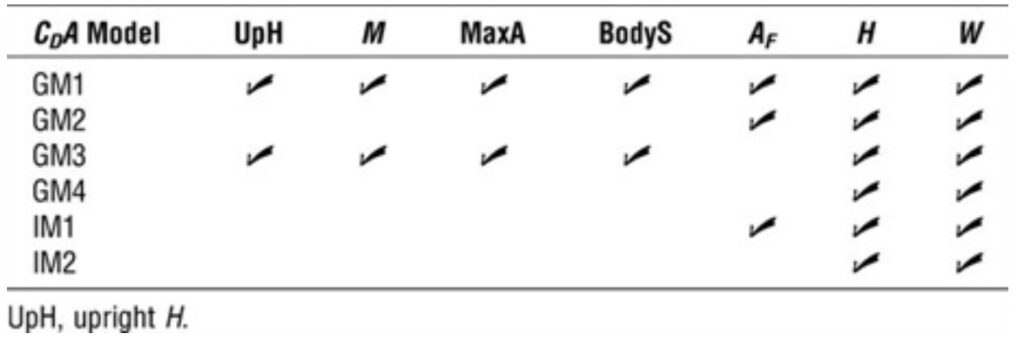
Tabella 1: una panoramica dei parametri inclusi nei sei modelli testati.
I parametri antropomorfi sono inerenti a un individuo e non variano con la posizione dello sciatore. Non sono quindi rilevanti per costruire modelli individualizzati. Tuttavia, l’uso di questi parametri può migliorare l’accuratezza dei modelli generalizzati.
- Esperimento sul campo
L’esperimento sul campo è stato condotto su una pista da sci al coperto. Uno dei 15 partecipanti si è offerto volontario per eseguire due piste da slalom gigante in un abito bianco punteggiato da pennarelli emisferici neri. Gli è stato chiesto di eseguire ampi movimenti attivi nella prima manche e di rimanere più compatto nella seconda manche. Sono state installate in totale sei porte con una distanza lineare di 24 metri e uno spostamento laterale di 9 m. Le prime tre porte sono state usate per iniziare a stabilire il ritmo e le ultime tre sono state registrate. L’angolo di inclinazione era di circa 8-10 gradi.
Per registrare la posizione dello sciatore durante la curva, sei telecamere piA1000-48gm con una risoluzione di 1004 × 1004 pixel e funzionanti a 48 Hz (Basler AG, Ahrensburg, Germania) sono state posizionate intorno al pendio, tre su ciascun lato. Gli orientamenti delle due telecamere superiore e inferiore erano fissi. Le due telecamere al centro sono state montate su teste di treppiedi appositamente costruite che hanno permesso agli operatori di spostarsi e inclinare le telecamere mantenendo le posizioni dei sensori della telecamera.
Prima del test quattro poli di calibrazione con tre marker ciascuno sono stati installati attorno al centro del volume di acquisizione e sono stati registrati con le telecamere. Una fotocamera è stata collegata tramite Gigabit Ethernet al proprio laptop, a un pacco batteria e a un’unità di sincronizzazione personalizzata. L’unità di sincronizzazione ha inviato segnali con la frequenza desiderata a ciascuna telecamera, attivando le telecamere per salvare le immagini nella memoria RAM dei loro laptop associati, utilizzando un software dedicato (SwisTrack; Lausanne, Svizzera). Quando l’unità di sincronizzazione era spenta o quando la memoria RAM era piena, tutte le immagini venivano trasferite sul disco rigido.
Le sequenze fornite dal sistema a telecamere multiple e le posizioni tridimensionali dei punti dati dalla stazione totale sono state elaborate utilizzando il software di movimento SIMI (SIMI Reality Motion Systems GmbH, Unterschleissheim, Germania). I marcatori di calibrazione sono stati inizialmente utilizzati per determinare gli 11 parametri standard del metodo di calibrazione della trasformazione lineare diretta (1).
I punti di riferimento sono stati apposti sul lato del padiglione per consentire di determinare gli angoli di panoramica e inclinazione delle telecamere durante le prove.
L’accuratezza della ricostruzione tridimensionale è stata controllata confrontando la posizione delle porte, data dalla stazione totale con la posizione calcolata con il software per le tre porte visibili sulle due piste. Il centro di M (CoM) dello sciatore è stato calcolato usando il metodo Hanavan (6).
Le traiettorie di posizione della testa, dei piedi e delle braccia sono state esportate per calcolare la H e la W dello sciatore.
- Analisi statistica
Una regressione lineare graduale all’indietro è stata utilizzata per trovare i migliori parametri predittivi dei modelli. Il valore di taglio per l’accettazione dei parametri è stato dichiarato a P ≤ 0,1. Sono stati calcolati il coefficiente di determinazione (R2) e la DS della stima dei modelli.
La convalida dei modelli generalizzati è stata eseguita rimuovendo un partecipante dal set di dati, ricalcolando i coefficienti del modello con i restanti 14 partecipanti e quindi utilizzando il partecipante rimosso per confrontare la previsione del modello con una misura indipendente. È stata eseguita una rotazione tra tutti e 15 i partecipanti e l’errore medio è stato usato per descrivere l’accuratezza del modello. I modelli individualizzati sono stati validati allo stesso modo, rimuovendo il risultato di una postura dal set di dati, ricalcolando il modello con le otto posture rimanenti e applicando i modelli alla postura rimossa.
I diagrammi di Bland-Altman (3) sono stati usati per confrontare l’accordo tra i modelli generalizzati e i dati sperimentali. Per i modelli generalizzati e individualizzati, è stato calcolato il limite di accordo del 95% (± 1,96 DS). Tutte le analisi statistiche sono state eseguite con il software SPSS 16 (SPSS, Inc., New York, NY) e la significatività è stata accettata a P <0,05.
Risultati
- Esperimento in galleria del vento
. Modelli sviluppati
La tabella 2 mostra il coefficiente di moltiplicazione di ciascun parametro, nonché R2, la SD della stima e la significatività di ciascun modello (P) sviluppato per stimare il CDA. Il taglio 0,1 dell’accettazione dei parametri ha scartato M, MaxA e BodyS da GM1, così come M e MaxA da GM3.

Tabella 2: coefficienti per i parametri dei modelli generalizzati e accuratezza dei modelli.
GM1 ha offerto la migliore precisione con R2= 0,972, P <0,001 e una DS della stima = 0,016 m2. Per GM2 e GM3, R2 era rispettivamente 0,962 (SD = 0,019 m2, P <0,001) e 0,953 (SD = 0,021 m2, P <0,001). Infine GM4 rappresentava il modello peggiore con un R2 pari a 0,933 (SD = 0,025 m2, P <0,001). I diagrammi di Bland-Altman tra i modelli generalizzati e i dati sperimentali sono mostrati nella Figura 2 per tutti i modelli generalizzati. Il limite del 95% dell’accordo è riportato anche per GM1 (± 11,00), GM2 (± 11,99), GM3 (± 13,25) e GM4 (± 14,18) nelle figure 2A, B, C e D, rispettivamente.
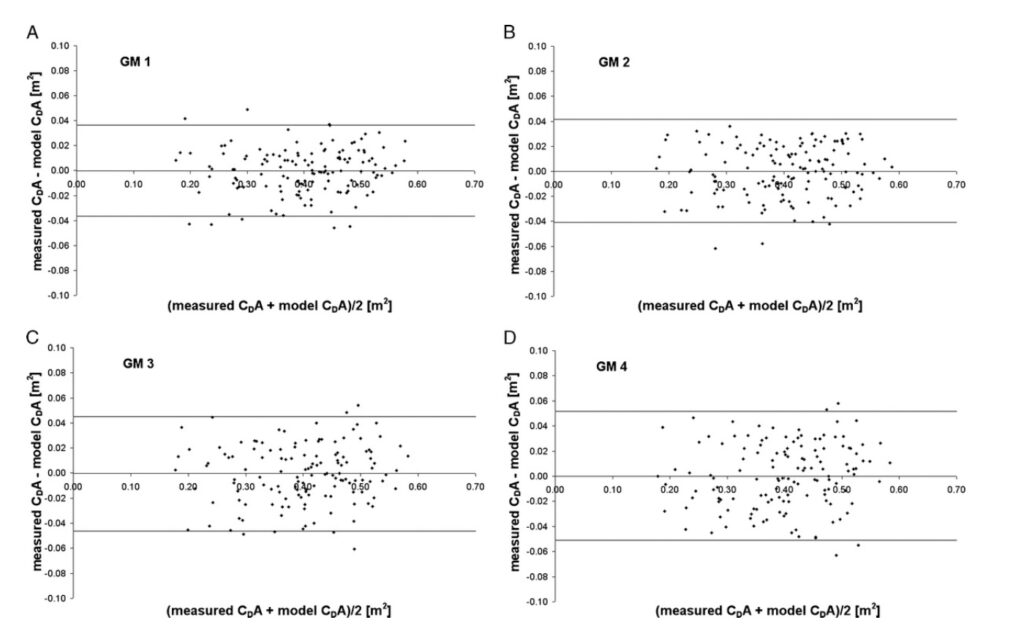
Figura 2: comparazione del CDA misurato e calcolato con modelli Balnd-Altman per i 4 modelli generalizzati. Le linee intere orizzontali rappresentano il 95% dei limiti di accordo.
Per i modelli individualizzati, la regressione lineare a posteriori non ha rimosso alcun parametro. IM1 ha raggiunto una media R2= 0,995 e una DS della stima= 0,009 m2. La convalida tra i modelli e le misure ha dato un limite di accordo del 95% di ± 4,52%. IM2 ha mostrato risultati leggermente peggiori con R2 = 0,989, SD = 0,01 m2 e un limite di accordo del 95% di ± 5,30%.
– Esperimento sul campo
Per stimare il suo CDA, il seguente IM2 è stato sviluppato individualmente per lo sciatore che ha eseguito il test sul campo:
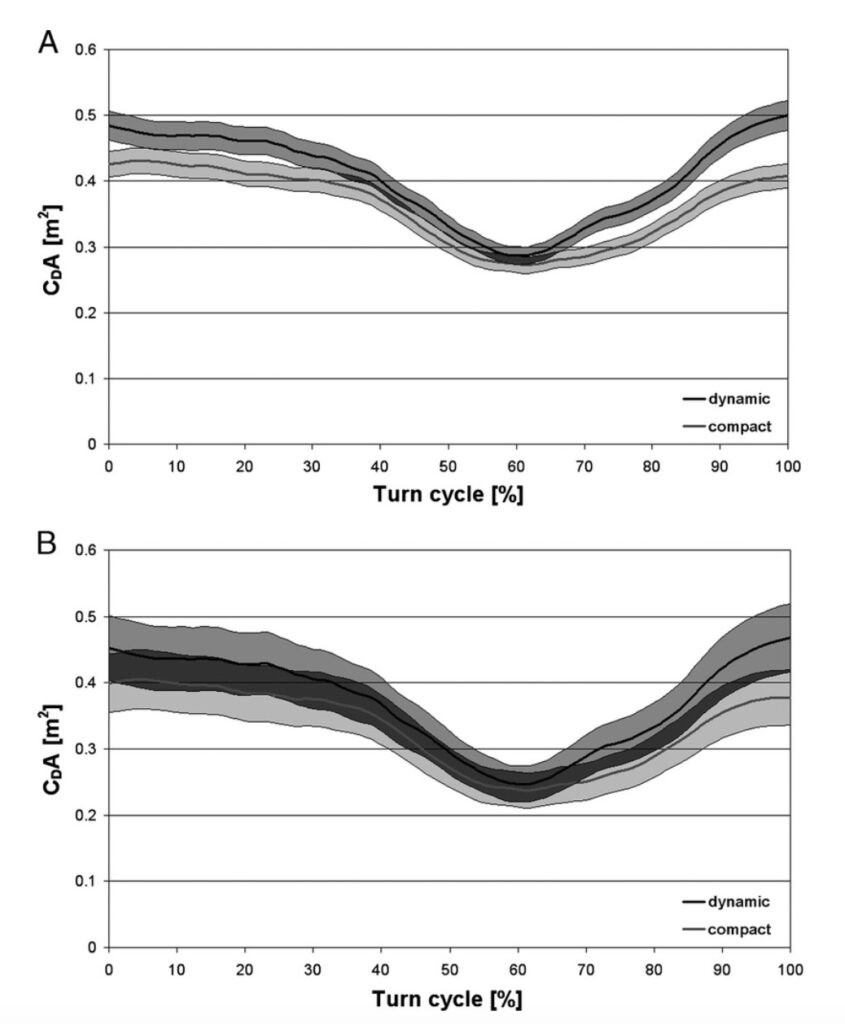
Figura 3A: confronta l’evoluzione del CDA su un ciclo di curva, usando l’IM2 definito nell’equazione 7, per le tecniche attive e compatte. Il limite di accordo del 5,30% indicato per l’IM2 è anche tracciato per ciascuna tecnica, mostrando una possibile differenziazione tra la tecnica di sci più dinamica e quella compatta per il 56% della curva. L’area grigia più scura indica una sovrapposizione del limite di accordo tra le due tecniche.
Figura 3B: mostra il confronto dello stesso set di dati, ma usando GM3. Il limite di accordo del 13,25% è anche tracciato per ciascuna tecnica, mostrando una sovrapposizione delle due tecniche durante l’intero curva.
L’equazione 5 fornisce l’energia totale dissipata a causa della resistenza aerodinamica ed è illustrata nella Figura 4 usando l’IM2 (Fig. 4A) o la GM3 (Fig. 4B) per una curva eseguita con le due diverse tecniche. Viene inoltre riportato il limite di accordo del 95%, che mostra la disparità di dissipazione di energia.
Per l’attuale slalom gigante, una tecnica attiva fornisce circa 3500 J di energia dissipata durante una porta. Ciò rappresenta circa 350 J in più di dissipazione di energia in una curva rispetto a una posizione compatta, il che significa una perdita del 10% in più di energia durante l’intera manche.
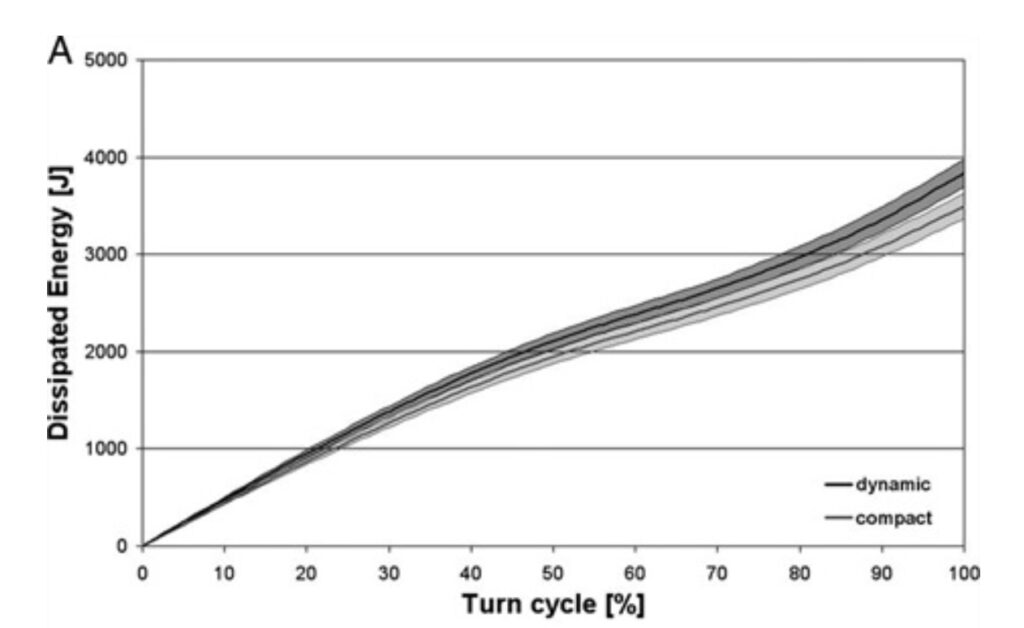
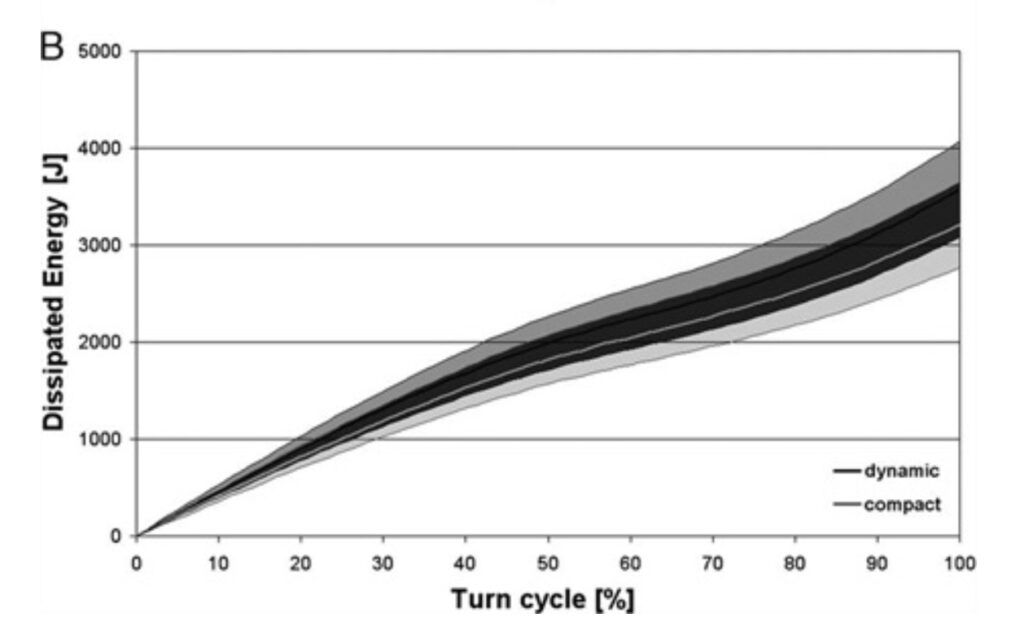
Figura 4: evoluzione dell’energia dissipata per via della resistenza aerodinamica sia per le tecniche compatte e dinamiche utilizzando il secondo modello individualizzato (A) e il terzo (B).
Discussione
La scoperta più importante di questo studio è l’accuratezza dei modelli individualizzati, che consentono un’ottima stima delle proprietà aerodinamiche degli sciatori durante l’esecuzione di curve di slalom gigante. In effetti questi modelli che spiegano il 98,9% e il 99,5% dei dati sperimentali, hanno un’accuratezza migliore del 5,30% per determinare il CD aerodinamico dello sciatore. L’accuratezza ottenuta è abbastanza buona per la discriminazione delle diverse tecniche eseguite da sciatori esperti, come mostrato nella Figura 3A.
I modelli generalizzati sviluppati sono un po’ meno precisi, spiegando tra il 93,3% e il 97,2% dei dati sperimentali, corrispondenti all’11,00% e al 14,18% di errore per il limite di accordo del 95%. L’uso di dati antropomorfi per costruire modelli generalizzati ha portato a un miglioramento solo del 2%. Pertanto le differenze di precisione di circa l’8% tra modelli generalizzati e individualizzati dovrebbero essere dovute ad altri fattori non misurati in questo studio come le differenze nella postura del corpo individuale mantenuta nella galleria del vento.
Simile al modello di Barelle e altri (2), i modelli generalizzati sviluppati in questa indagine consentono un confronto intra-individuale globale di uno sciatore che esegue tecniche diverse, ma non una differenziazione accurata tra sciatori. Tuttavia i parametri utilizzati in questo studio sono meno specifici delle lunghezze e degli angoli dei segmenti utilizzati da Barelle e altri (2) e offrono un uso più ampio e più generico dei modelli. Ciò consente al metodo di regressione lineare a posteriori di scegliere i parametri pertinenti e rifiutare i parametri non necessari per il modello. È quindi possibile una maggiore flessibilità per l’ulteriore integrazione dei parametri. Barelle e altri (2) hanno considerato molte più posizioni per consentire la variazione dei diversi parametri, ma alla fine il CD trovato in entrambi gli studi corrisponde molto bene alle diverse posizioni che uno sciatore può raggiungere durante una discesa.
I modelli sviluppati aiutano a comprendere i fattori intrinseci della dissipazione di energia calcolati da Supej (16) e Reid e altri (11). Entrambi hanno trovato un’elevata dissipazione di energia a livello porta e una bassa dissipazione di energia durante la transizione (dinamica) dalla porta, che è invertita rispetto alle curve di Eaero nella Figura 4. La dissipazione di energia dovuta all’attrito della neve, stimata da Meyer e Borrani (10), indica un maggiore importanza dell’attrito sci-neve nello slalom gigante e curve corrispondenti ai risultati ottenuti da Supej (16) e Reid e altri (11).
Lo studio condotto qui è una prima approssimazione della resistenza aerodinamica dello sciatore, che è corretta sul campo in caso di velocità del vento ambientale ridotta o assente. In questo caso il flusso del vento sullo sciatore sarà sempre diretto davanti, indipendentemente dalla sua direzione di marcia (nessun angolo di incidenza). Se la velocità del vento è notevole, la resistenza aerodinamica vissuta dallo sciatore cambierà in base alla sua direzione di marcia (angolo di incidenza diverso da zero). Per modellare questo scenario, ulteriori test dovrebbero essere condotti in una gamma di angoli di incidenza di uno sciatore nella galleria del vento. Quindi un nuovo modello dinamico potrebbe calcolare la resistenza aerodinamica dello sciatore considerando la velocità del vento e la direzione relativa e l’angolo di contatto dello sciatore in ciascun punto della curva. Al contrario per piccoli angoli di incidenza il modello attuale serve come una buona stima della resistenza aerodinamica.
Una limitazione del metodo attuale è che le varie posture nella galleria del vento utilizzate per sviluppare i modelli (Fig. 1) sono simmetriche e differiscono dalle posizioni asimmetriche dello sciatore ottenute durante la curva, un fatto che potrebbe compromettere la validità del modello. Sfortunatamente la ripetibilità di mantenere posture più specifiche nella galleria del vento era scarsa a causa della difficoltà di mantenere posizioni sbilanciate.
Una seconda limitazione è che i modelli riportati utilizzano le misurazioni della galleria del vento di una serie di posizioni statiche per modellare gli sciatori che cambiano continuamente posizione mentre curvano. Può darsi che il comportamento dinamico della resistenza aerodinamica di uno sciatore in movimento continuo possa in qualche modo differire da quello di una serie di posizioni statiche.
Tuttavia le misurazioni in galleria del vento sono attualmente limitate a posizioni statiche poiché la piattaforma delle forze di terra registrerebbe ogni accelerazione CoM, rendendo difficile isolare l’aerodinamica D.
In conclusione questo articolo fornisce modelli semplici e funzionali per calcolare la resistenza aerodinamica degli sciatori che eseguono curve di slalom gigante. I modelli sviluppati offrono una precisione media compresa tra il 4,52% e il 14,18%, a seconda dei parametri selezionati. L’uso di questi modelli negli studi sul campo di sci può aiutare a migliorare la nostra comprensione del ruolo della resistenza aerodinamica nelle prestazioni degli sciatori. Un modello funzionale di attrito sci-neve durante le curve deve ancora essere sviluppato per avere una visione completa di dove, come e quando gli atleti perdono energia durante le curve.
Tratto da :
MEYER F., LE PELLEY D., BORRANI F. “Aerodynamic Drag Modeling of Alpine Skiers Performing Giant Slalom Turns”. Medicine & Science in Sports & Exercise: June 2012 – Volume 44 – Issue 6 – pp.1109-1115
Riferimenti bibliografici
1. Abdel-Aziz YI, Karara HM. Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry. In: Proceedings of the American Society of Photogrammetry Symposium on Close-Range Photogrammetry. 1971. p. 1–8.
2. Barelle C, Ruby A, Tavernier M. Experimental model of the aerodynamic drag coefficient in alpine skiing. J Appl Biomech. 2004; 20: 167–76.
3. Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986; 1 (8476): 307–10.
4. Boyd E. The Growth of the Surface Area of the Human Body. Minneapolis (MN): University of Minnesota Press; 1935. p. 52–112.
5. Flay J, Vuletich IJ. Development of a wind tunnel test facility for yacht aerodynamic studies. J Wind Eng Ind Aerodyn. 1995; 58 (3): 231–58.
6. Hanavan EP Jr. A mathematical model of the human body. AMRL-TR-64-102. AMRL TR. 1964: 1–149.
7. Kaps P, Nachbauer W, Mössner M. Determination of kinetic friction and drag area in alpine skiing. In: Ski Trauma and Skiing Safety. 10th ed. 1996. p. 165–77.
8. Lopez JG, Rodriguez-Marroyo JA, Juneau CE, Peleteiro J, Martinez AC, Villa JG. Reference values and improvement of aerodynamic drag in professional cyclists. J Sport Sci. 2008; 26 (3): 277–86.
9. Luethi S, Denoth J. The influence of aerodynamic and anthropometric factors on speed in skiing. J Appl Biomech. 1987; 3: 345–52.
10. Meyer F, Borrani F. 3D model reconstruction and analysis of athletes performing giant slalom. In: Abstract Book of the 5th International Congress on Science and Skiing; St. Christoph am Arlberg (Austria). 2010. p. 64.
11. Reid R, Gilgien M, Moger T, et al.. Turn characteristics and energy dissipation in slalom. In: Lindinger S, Müller E, Stöggl T, editors. Science and Skiing IV. Maidenhead: Meyer & Meyer Sport (UK), Ltd.; 2009. p. 419–29.
12. Savolainen S. Theoretical drag analysis of a skier in the downhill speed race. J Appl Biomech. 1989; 5: 26–39.
13. Sayers AT, Ball DR. Blockage corrections for rectangular flat plates mounted in an open jet wind tunnel. Proc Inst Mech Eng C J Mech Eng Sci. 1983; 197: 259–63.
14. Shanebrook JR, Jaszczak RD. Aerodynamic drag analysis of runners. Med Sci Sports. 1976; 8 (1): 43–5.
15. Spring E, Savolainen S, Erkkila T, Hamalainen T, Pihkala P. Drag area of a cross country skier. J Appl Biomech. 1988; 4: 103–13.
16. Supej M. Differential specific mechanical energy as a quality parameter in racing alpine skiing. J Appl Biomech. 2008; 24 (2): 121–9.
17. Thompson BE, Friess WA, Knapp KN 2nd. Aerodynamics of speed skiers. Sports Eng. 2001; 4: 103–12.
18. van Ingen Schenau GJ. The influence of air friction in speed skating. J Biomech. 1982; 15 (6): 449–58.
19. Watanabe K, Ohtsuki T. Postural changes and aerodynamic forces in alpine skiing. Ergonomics. 1977; 20 (2): 121–31.
20. Watanabe K, Ohtsuki T. The effect of posture on the running speed of skiing. Ergonomics. 1978; 21 (12): 987–98.
